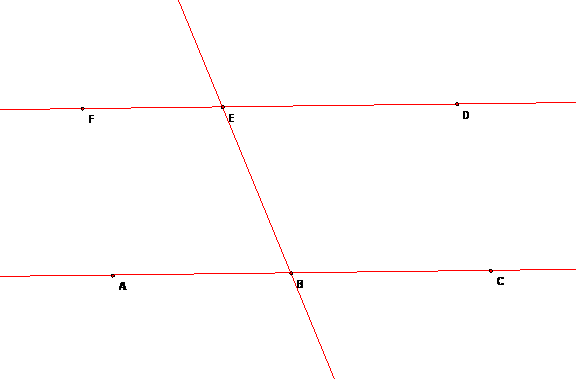
Suppose in the figure that angle ABE = angle DEB.  What can you say about the other angles?  Why?

Now suppose that the angles are still equal as before, but that the lines intersect at A.  We will show that this implies the lines intersect at TWO points, a contradiction.

Parallel Postulate:  For any line AB and any point E not on the line, then there is exactly one parallel to line AB through E.

Corollary.   If points B and E are on parallel lines, then the alternating interior angles formed by BE and the parallel lines are equal.  Also, all the other relationships in the first figure then hold.

Theorem.  The sum of the angles in any triangle equals a straight angle (180 degrees).

Proof:  Given a triangle ABC, construct the line through C parallel to AB.  Then note the equal angles.